Chapter 9 Application Project:

Keeping Time Is Timeless

In this project, we will examine a pendulum that uses the solution of the tautochrone problem discussed in Section 9.1. Such a pendulum was invented as early as 1657 by the Dutch mathematician, physicist, and astronomer Christiaan Huygens (1629–1695). Huygens was interested in developing accurate clocks, and thus needed a pendulum whose period of oscillation was independent of amplitude (i.e., unaffected by the initial position of the pendulum bob when released to swing freely). Huygens' work, Horologium Oscillatorium (published in 1673) as well as his numerous other groundbreaking findings in various areas of mathematics, physics, engineering, and astronomy, are a testament to his brilliance and creativity. We will analyze his invention by appropriately modifying the parametric equations of the cycloid introduced in Example 4 of Section 9.1.

1. 1. Sketch the inverted cycloid traced out by a point P on a circle of radius a that rolls counterclockwise along the line $y=2a$ assuming that P starts out at $\left(0,2a\right)$. (The circle is positioned between the x-axis and $y=2a$.) Show the path traced out by P after two full revolutions; that is, sketch the cycloid on the parametric interval $0\le \theta \le 4\pi$.

   2. Make a sketch to show the inverted cycloid of part a. on the parametric interval $-\pi \le \theta \le \pi$.

2. 1. Find the parametric equations of the inverted cycloid (henceforth referred to simply as cycloid) in Question 1.

   2. Use technology to reproduce the graph you sketched in Question 1b.

3. Now, suppose we create a pendulum by attaching a cord of length $4a$ to the cusp located at $\left(0,2a\right)$ of the cycloid of Question 1b, and let the bob swing left and right, partially wrapping the cord around the cycloid in the process (see Figure 1).

   

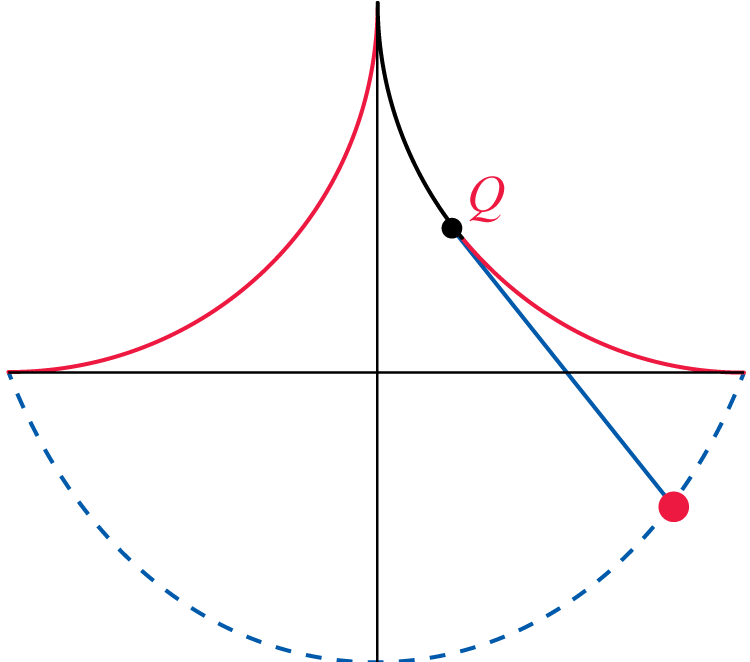
   An unlabled cartesian plane. A dashed semi-circle lies beneath the x-axis ranging from quadrant 3 to quadrant 4. Quadrants 1 and 2 both contain a quarter-circle, starting at the end points of the semi-circle, curving inward towards the origin, and meeting at a cusp on the y-axis. In quardrant 1, a section from the cusp to a point labeled Q is highlighted on the quarter-circle. A line then extends from point Q to an unlabeled point on the semi-circle in quadrant 4.

   Source: Wolfram Demonstrations Project

   1. Given that the length of the cord is equal to $4a$, where does the bob touch the cycloid at the pendulum's most extreme positions? That is, what is the location of the bob when the cord is completely wrapped around the cycloid? (Hint: See Example 7 in Section 9.2.)

   2. Note that while the pendulum is moving, the "free" part of the cord (the portion that is not wrapped around the cycloid) is tangent to the cycloid. Let Q denote the point of tangency (see Figure 1), and suppose that Q corresponds to the parameter value ${\theta }_0$. Find the length s of the portion of the cord that is wrapped around the cycloid under these conditions. (Hint: Make a detailed sketch and consider the angle that the tangent of the cycloid forms with the x-axis. See Exercise 71 in Section 9.2.)

4. 1. Use your work on Question 3b to obtain a parametrization of the path traced out by the bob of the pendulum. (Hint: First find x and y in terms of $\theta$ and s; then eliminate s by making use of the formula you found in Question 3b.)

   2. What kind of parametric curve have you obtained in part a.? Use your answer to conclude that the cycloidal pendulum is tautochronous; that is, its period of oscillation is independent of amplitude. (See the discussion and derivation under Topic 2 in Section 9.1.)