Dream Plans
Owning your own home has always been part of the American Dream. But how feasible is building that home? In this project, you will use Pólya's problem-solving process to estimate the cost of building a house. Assume that you already own the land the house will be built on, and the neighborhood has the following building restrictions.
The house must meet the following parameters:
-
Square footage: to
-
Bedrooms: to
-
Bathrooms: to
-
Other required rooms: kitchen, dining area, living room, laundry room
Step 1: Understand the Problem
-
The first step is to identify what is being asked of you for this project. Describe in your own words the goal of this project and the steps you will take to complete the project.
Step 2: Devise a Plan
-
List the different aspects of building a house from initial design to finalizations. Be sure to consider both physical labor required and materials to be purchased. (Note: You do not need to list specific costs, only the categories.)
-
Do some research to determine an estimated cost per square foot. Describe what considerations went into estimating the overall cost. Be sure to state where the house will be built.
Step 3: Carry Out the Plan
-
Determine the number of bedrooms, bathrooms, and total square footage of your home. Include the dimensions of the rooms and as much detail as possible.
Step 4: Look Back
-
Determine a rough estimate for the cost of the house designed in Step 3 and the cost per square foot from Step 2.
-
How does the estimated cost of your house compare with the real estate market in your city or town? What source(s) did you use to make the comparison?
-
Name at least two factors that might cause the cost of building your house to be more than you estimated. Explain how you can decrease the cost of building the house.
-
Name at least two things you learned in the process about building a house.
-
What would you change about your original house plan based on your findings?

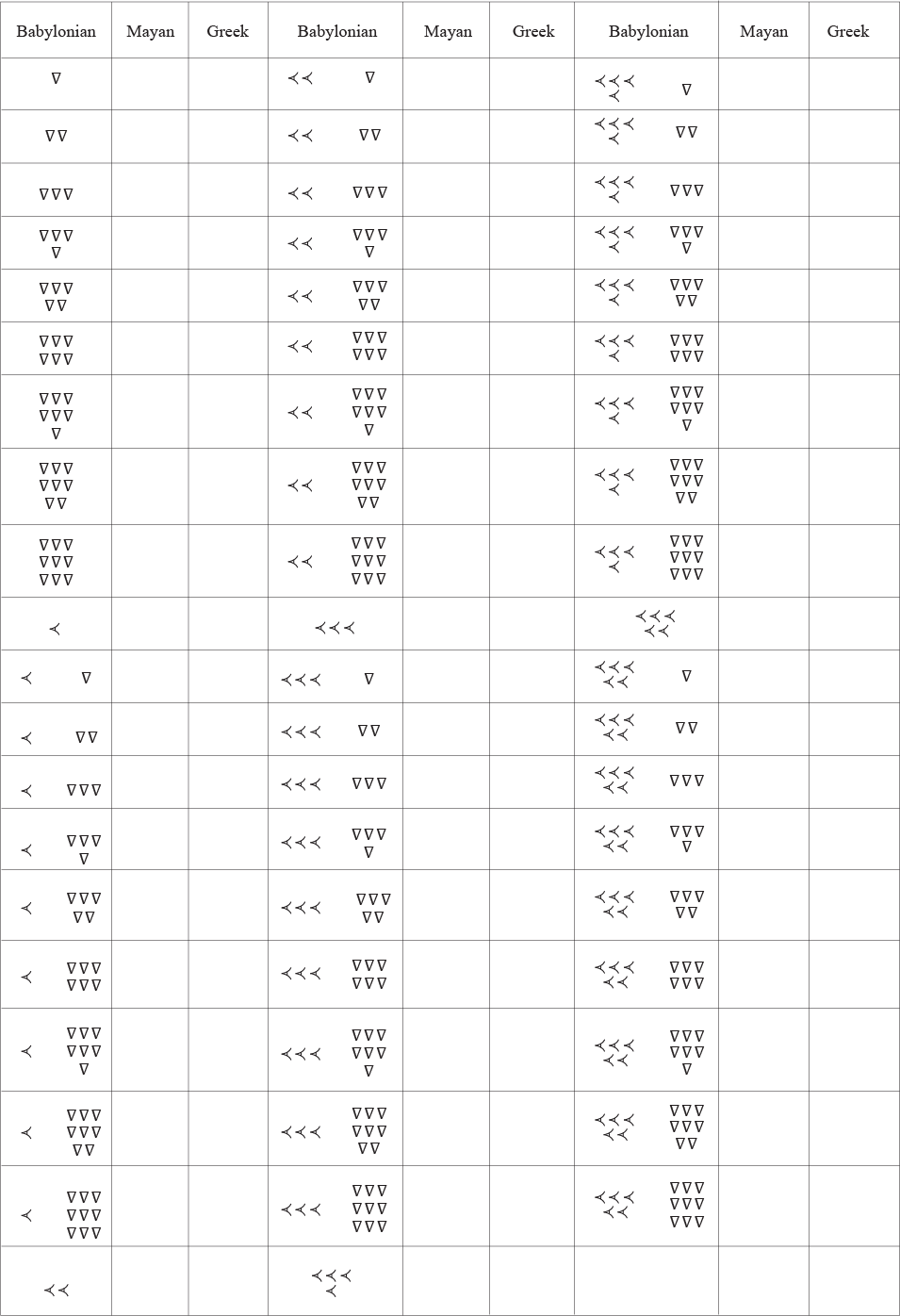
 bales of hay for
bales of hay for
 gold coins. Convert these values to both the Mayan and the Greek system.
gold coins. Convert these values to both the Mayan and the Greek system.